Dynamic Programming :computer:

Prerequisites: Preliminaries Hello-world

In this exercise you will implement Value and Policy iterations to solve a particular stationary Markov Decision Process (MDP).

You are an operator on a distant planet at a base responsible for deploying autonomous survey robots looking for unobtainium. Your job is to send a surveying robot to a location specified by your company’s client.

For each contract, you can deploy several robots, but only one at a time - corporate requires you to have at most one active robot in the field at any given time to try to save money. You can always choose to abandon an active robot and deploy a new one from the base. In some cases, an active robot might break down - then, you are forced to abandon it. However, deploying the second and every next robot for a contract costs you money (the first robot is covered by the client).

Once a robot reaches the goal location, it stays there and delivers data reports to the client, thus fulfilling the contract. For this, you receive a reward from the client. Your robot should reach the goal location as fast as possible since the client is entitled to compensation for the time it takes you to fulfill the contract.

Your task is to create a plan for each given contract that maximizes your profit. You choose to model this problem as a Markov Decision Process (MDP) and use dynamic programming to compute offline the optimal policy for each mission.

Problem description

The world is modeled as a 2D grid, which is represented through a MxN matrix (numpy array). Rows and columns represent the $i$ and $j$ coordinates of the robot, respectively. The area around you is a tropical rainforest, which can be modeled in the grid with the following types of cells:

The time required to cross each cell corresponds to the time a robot needs to leave this cell (e.g. leaving the START cell takes 1 hour). When in a specific cell, you can plan for the robot to take one of the following actions:

The goal of your policy is to maximize profit (use 1k USD as the default unit):

The planet’s atmosphere is very foggy and when the robot decides to move in a specific direction, it may not end up where initially planned. Sometimes, when trying to move, it might also break down and be forced to abandon its mission. In fact, for all transitions, the following probabilities are given:

If the robot breaks down or chooses to ABANDON the mission, a new robot is deployed in the START cell, which costs you 10k USD.

Hints

Tasks

Data structure

Actions, states, Value function and Policy are defined as follows (exercises/ex04/structures.py):

from enum import IntEnum, unique
from typing import Union

import numpy as np
from numpy.typing import NDArray


@unique
class Action(IntEnum):
    NORTH = 0
    WEST = 1
    SOUTH = 2
    EAST = 3
    STAY = 4
    ABANDON = 5


State = tuple[int, int]
"""The state on a grid is simply a tuple of two ints"""


@unique
class Cell(IntEnum):
    GOAL = 0
    START = 1
    GRASS = 2
    SWAMP = 3
    WORMHOLE = 4
    CLIFF = 5


Policy = NDArray[np.int64]
"""Type Alias for the policy.It is the expected type of the policy that your solution should return."""
OptimalActions = NDArray[np.object_]
"""
Type Alias for the all optimal actions per state. It is a numpy array of list objects where each list contains the
optimal actions that are equally good for a given state. It is the type of the ground truth policy that your
solution will be compared against. You are not required to use this type in your solution.
"""
ValueFunc = NDArray[np.float64]
"""Type Alias for the value function. It is the expected type of the value function that your solution should return."""

The first subtask is to implement the missing methods in exercises/ex04/mdp.py. These methods will be useful when implementing value and policy iteration.

class GridMdp:
    def __init__(self, grid: NDArray[np.int], gamma: float = 0.9):
        assert len(grid.shape) == 2, "Map is invalid"
        self.grid = grid
        """The map"""
        self.gamma: float = gamma
        """Discount factor"""

    def get_transition_prob(self, state: State, action: Action, next_state: State) -> float:
        """Returns P(next_state | state, action)"""
        # todo

    def stage_reward(self, state: State, action: Action, next_state: State) -> float:
        # todo

Feel free to add more methods in case you need to. The method get_transition_prob returns the probability of transitioning from a state to another given an action. The method stage_rewardreturns the reward that corresponds to transitioning from the current state to the next after choosing the given action.

Value Iteration

We’ll start with value iteration. You need to implement the following methods in exercises/ex04/value_iteration.py:

class ValueIteration(GridMdpSolver):
    @staticmethod
    @time_function
    def solve(grid_mdp: GridMdp) -> Tuple[ValueFunc, Policy]:
        value_func = np.zeros_like(grid_mdp.grid).astype(float)
        policy = np.zeros_like(grid_mdp.grid).astype(int)

        # todo implement here

        return value_func, policy

Policy iteration

For policy iteration, you need to implement the following methods in exercises/ex04/policy_iteration.py:

class PolicyIteration(GridMdpSolver):

    @staticmethod
    @time_function
    def solve(grid_mdp: GridMdp) -> Tuple[ValueFunc, Policy]:
        value_func = np.zeros_like(grid_mdp.grid).astype(float)
        policy = np.zeros_like(grid_mdp.grid).astype(int)

        # todo implement here

        return value_func, policy

Expected outcome

For both Value and Policy iterations, you need to return the optimal ValueFunc and one of the optimal Policy for the given MDP.

Note: The optimal value function is unique, but the optimal policy is not. You can return any optimal policy that satisfies the Bellman optimality equation.

To keep the format consistent, the value function and policy should be returned as MxN matrices (numpy arrays) where each cell corresponds to the value of the state or the action to be taken in the state, respectively. The value function and policy of CLIFF cells will be excluded for evaluation.

If your algorithm works, in the report you should find some results similar to this:

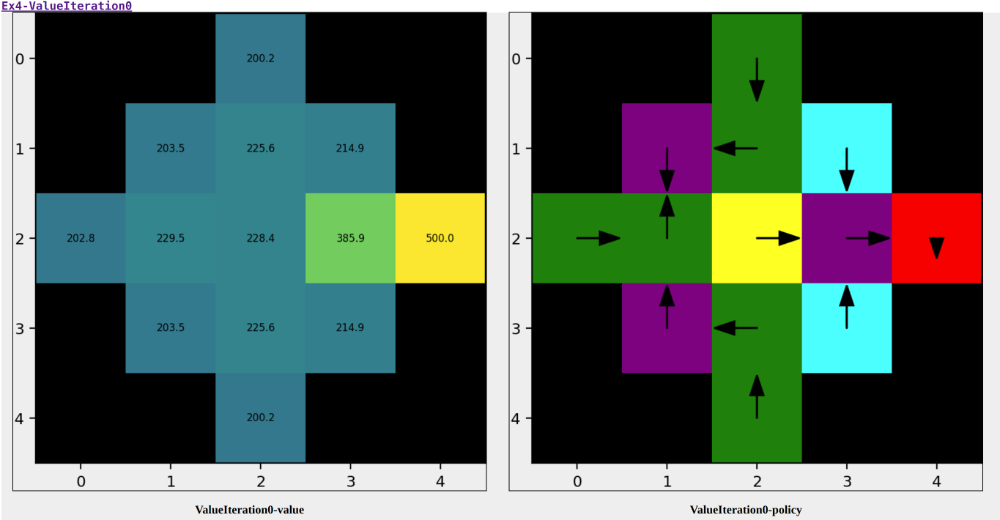
image

Figure 1: Visualization of the optimal value function and policy for a 5x5 example.

On the left the Value function is visualized as a heatmap. On the right you can see the map with the original cells and the corresponding optimal policy (arrows for movement actions, X for the ABANDON action).

Help for modeling the MDP

Correctly modeling the MDP is crucial for the success of your algorithms. To help you with this, we provide you with the admissible action set, the ground truth transition probabilities and rewards for selected cells of the 5x5 example above. You can use these to validate your implementation.

The coordinates of the cells are given in the format (row, column) starting from the top left corner of the grid. All axes are 0-indexed.

Admissible action set

Note: The admissible action set is only given for a selection of states.

<current state>: [list of admissible actions]

- (0, 2): [SOUTH, ABANDON]  
- (1, 2): [WEST,EAST ,NORTH, SOUTH, ABANDON]
- (1, 1): [SOUTH, EAST, ABANDON]
- (3, 3): [WEST, NORTH, ABANDON]

Ground truth transition probabilities and rewards

Note: The ground truths are only given for a selection of state-action pairs.

(<current state>, <action>): (<next state>, <probability>, <reward>)

- ((0, 2), SOUTH):   ((1, 2), 0.75, -1), ((2, 2), 0.25, -11)
- ((0, 2), ABANDON): ((2, 2), 1.0, -10)
- ((1, 2), WEST):    ((3, 1), 0.25, -1), ((1, 1), 0.25, -1), ((2, 3), 0.25, -1), ((0, 2), 0.0833, -1), ((2, 2), 0.0833, -1), ((1, 3), 0.0833, -1)
- ((1, 1), SOUTH):   ((1, 2), 0.0833, -1), ((2, 1), 0.75, -1), ((2, 2), 0.1667, -11)
- ((3, 3), WEST):    ((3, 1), 0.02778, -2), ((1, 1), 0.02778, -2), ((2, 3), 0.02778, -2), ((2, 2), 0.21667, -12), ((3, 2), 0.5, -2), ((3, 3), 0.2, -2)

Test cases and performance criteria

The algorithms are going to be tested on different MDPs, each containing randomly located queries (start & goal cells). You will be able to test your algorithms on some test cases with given solution, the outputted Policy and ValueFunc will be compared to the solution. After running the exercise, you will find the reports in out/04/ for each test case. There you will be able to visualize the MDPs, your output and the expected solution. These test cases are not graded but serve as a guideline for how the exercise will be graded overall.

The final evaluation will combine the following metrics: ratio of completed cases, average policy_accuracy, average value_func_R2, and average solve_time:

The final score will be computed as follows: $score = \frac{N_{completed}}{N} \cdot (\frac{policy_accuracy + value_func_R2}{2} - 0.0025 \cdot solve_time)$

In the report you will find the average of each metric for all the test cases (perf_result), value iteration test cases (value_iteration) and policy iteration test cases (policy_iteration). The score is calculated based on all the test cases (perf_result).

Update your repo and run exercise

Make sure to update your repo before running the exercise. Please refer to Hello World for instructions.